Which Trigonometric Functions Have a Defined Amplitude
See if you can figure out why. The amplitude is the distance between the centerline of the function and the maximum or minimum point of the function.

Understanding Hertz Netwell Ultrasound Physics Physics And Mathematics College Physics
Amplitude only makes sense on the sine and cosine graphs.

. Graphing And Inverse Functions. Y sin2Pit frequency 1. PERIOD A function f with domain set S is periodic if there exists a positive real.
Y sint basic sine function. The usual period is 2 π but in our case that is sped up made shorter by the 4 in 4x so Period π 2. Which trigonometric functions have a defined amplitude.
In this case our function has been multiplied by 4. Y sint2 time shift of -2. Select all that applysine cosine tangent cosecant secant cotangent sine cosine tangent cosecant secant cotangent.
Sine functions fx a sinx and cosine functions fx a cosx have positive amplitudes of a. All sine functions have an amplitude and a period. If an answer is undefined enter UNDEFINED 180 sin 180 cos 180º tan 180 - cot 180 sec.
41 Basic Graphs 42 Amplitude Reflection And Period 43 Vertical And Horizontal Translations 44 The Other Trigonometric Functions 45 Finding An Equation From Lts Graph 46 Graphing Combinations Of Functions 47 Inverse Trigonometric Functions Chapter Questions expand_more. This can be found by finding the range of the function and dividing by two. And the 05 means it will be shifted to the right by 05.
Think of the effects this multiplication has on the outputs. Y 2cost doubled amplitude. Amplitude A 2.
One cycle per second is given a special name Hertz Hz. Select all that apply 61031 points Previous Answers McKTrig7 41008. Use the unit circle to find the six trigonometric functions of the angle.
The 2 tells us it will be 2 times taller than usual so Amplitude 2. Sin x cos x tanx cot x sec x and csc x are discussed. Y 2sint doubled amplitude.
Amplitude and Period of a Tangent Function The tangent function does not have an amplitude because it has no maximum or minimum value. Y sin2t doubled frequency. Y cos2t doubled frequency.
Trigonometric graphs have four key features. All real numbers Range. Phase shift 05 or 05 to the right vertical shift D 3.
I sometimes describe it as a pseudo-amplitude because it can be used in a similar way in graphing. While this number is -24 we always represent amplitude as a positive number by taking the absolute value of it. Which trigonometric functions have a defined amplitude.
Select all that apply O sine O cosine tangent O cosecant O. The amplitude of the parent function is 1 since it goes from -1 to 1. The graph of an even function is symmetric about the _____ and the graph of an odd function is symmetric about the _____.
Y cost2 time shift of. AMPLITUDE the maximum height of the curve. What are the key features of the graphs of trigonometric functions.
We can also consider the amplitude as the vertical distance between the sinusoidal axis and the maximum or minimum values of the function. The amplitude is half the distance between the maximum and minimum values of the graph. The parent functions fx sinx and fx cosx have an amplitude of 1 reaching heights of a maximum of 1 above the x-axis and below the x-axis.
Trigonometric functions are also known as Circular Functions can be simply defined as the functions of an angle of a triangle. It means that the relationship between the angles and sides of a triangle are given by these trig functions. It also have a frequency of 1s.
Up to 10 cash back When you think of a trigonometric function of the form y A s i n B x C D the amplitude is represented by A or the coefficient in front of the sine function. The amplitude is the distance from the midline to the maximum or to the minimum they are the same. Its frequency and period can be determined when written in this form.
The properties of the 6 trigonometric functions. Trigonometric Curves with Sines Cosines Envelopes. Select all that apply sine O cosine tangent cosecant secant cotangent 2-1 pointsMcTrig8 33023.
Other trig functions like MATHAtan BxCD MATH have a scale factor MATHA MATH that is not an amplitude because it does not represent a maximum deviation from the base value MATHD MATH. The basic trigonometric functions are sine cosine tangent cotangent secant and cosecant. A sin function repeats regularly.
71031 points Previous AnswersMcKTrig7 41009. For any periodic function the amplitude is defined as M m2. So we have signed Co.
Period 2 π B 2 π 4 π 2. Where M is the maximum value and m is the minimum value provided they exist. Cosine based graphs y cost basic cosine.
Therefore the amplitude of this function is 24. -1 1 Period 2pi. So lets just first write down all the trees geometric functions.
Which trigonometric functions have asymptotes. Sign the tangent the CO second the second and the coat ancient. Fx sin x Graph.
These include the graph domain range asymptotes if any symmetry x and y intercepts and maximum and minimum points. Yt sin2pi f t. Something that repeats once per second has a period of 1 s.
Now note that sign and go sign. Also see Trigonometric Functions. The amplitude is the distance from the midline to either the top or bottom of the graph.
Sine cosine Which trigonometric functions have a defined amplitude. Trigonometry questions and answers. Amplitude of Functions.
So the ones that have me defined the amplitude mhm our sign and causing. And in this problem we have to name the trick geometric functions that have as um Dotes. The amplitude of a function describes its height from the midline to the maximum.
The period of a tangent function yatanbx is the distance between any two consecutive vertical asymptotes. Amplitudes are always positive because they are distances 1. Up to 10 cash back Possible Answers.
You may also say that it has a frequency of 1 Hz. Today Ill be going over question number seven which talks about the trigger metric functions that have defined attitude. In a formula form the amplitude is the coefficient in front of the trig function.
The function is generally represented as yA sin B xCD Here A rightarrow alters the amplitude of the wave in y-direction above and below the x-axis. Which trigonometric functions have a defined amplitude. For example y sinx has an amplitude of 1 because the midline is y0 and the max is 1.

Amplitude Period And Frequency Ck 12 Foundation

Amplitude And Period Explained Teaching Algebra Learning Mathematics Math Genius
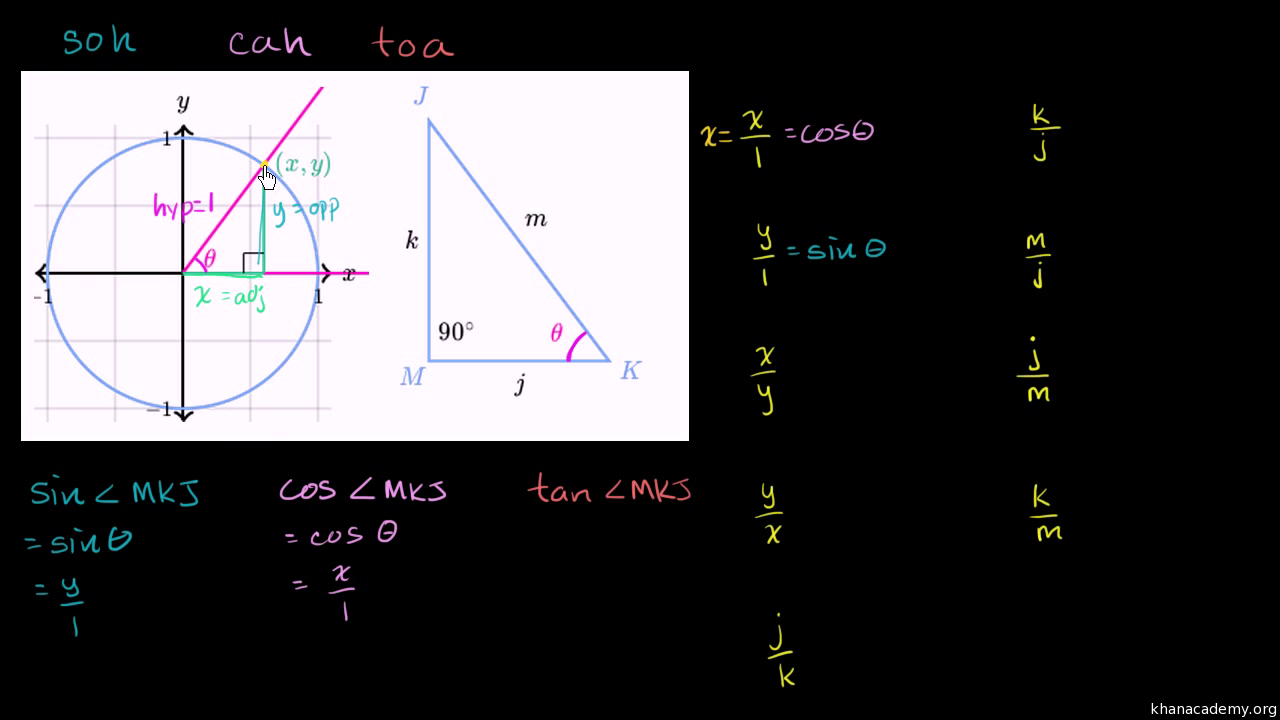
Trigonometric Functions Algebra All Content Math Khan Academy

Pin By Brian Lopez On Math Math For Kids Fun Math Math Tutor

This Lesson Is Designed For Precalculus Students For The Unit On Applications Of Trigonometry In This Lesson Stu Precalculus Parametric Equation Trigonometry
Solved Which Trigonometric Functions Have A Defined Amplitude

Sinusoidal Functions Waterford District High School Secondary Math Math Lesson Plans Calculus

Amplitude Period And Frequency Ck 12 Foundation

Amplitude Period And Frequency Ck 12 Foundation

Graphing The Sine And Cosine Digital Assignment Distance Learning Graphing Secondary Math

Solved Which Trigonometric Functions Have A Defined Chegg Com

End Of Course Review And Exam For Trigonometry Or The Trig Units Of Precalculus Over 92 Different Questions In 3 Formats Trigonometry Task Cards Precalculus

Solved Which Trigonometric Functions Have A Defined Chegg Com

Solved 1 1 Pointsmck Trig8 4 1 007 Which Trigonometric Chegg Com




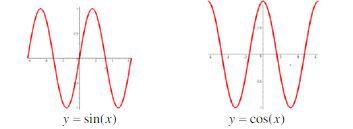
Comments
Post a Comment